1. 가설
input variable(또는 feature)과 output(또는 target variable)의 관계를 나타내는 함수.
다음과 같은 집값 데이터를 수집했다고 하자.
| 집 크기(m²) | 집 값(₩) |
| 195 | 507840000 |
| 132 | 256128000 |
| 142 | 347760000 |
| 79 | 196512000 |
- 집 크기는 input, 집 값은 output에 해당한다.
- 집 값 예측: input(집 크기)와 output(집 값)의 관계식을 정의해 새롭게 주어지는 집 크기에 대한 집 값을 예측한다.
- 이 때의 관계식이 '가설(hypothesis)'에 해당한다.
* 관계식을 '가설'이라고 하는 이유
집 값 예측: 집 값을 도출해낼 수 있는 변수(feature)와 집 값(output)의 관계식을 정의한다.
- feature를 정확히 정의할 수 있는가
집 값에 영향을 미치는 요인은 집 값 뿐만 아니라 정치권의 행보, 집의 위치, 인프라 등 무수히 많은 요인이 있다.
-> 따라서 이런 무수히 많은 변수와 그 변수들 간의 복잡한 관계식을 찾는 대신 '주로 이런 변수들이 output에 영향을 미칠 것'이라고 추정하고 '변수들과 output의 관계를 이러이러한 함수로 얼추 표현할 수 있을 것'이라고 "가설"을 세우는 것이다.
- 가설은 주로 다음과 같이 일차 함수(선형 함수, linear function)의 형태로 정의한다.
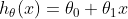
$x$: feature(여기서는 집 크기)
$h_{\theta}(x)$: output(여기서는 집 값)
$\theta_{i}$: 가설의 parameter
- 위의 가설은 feature가 하나일 때(Univariable linear regression 또는 Linear regression with one variable)의 가설이기 때문에 매우 간단한 형태지만, feature가 여러 개일 때는 다음과 같이 약간 복잡해진다.
$h_{\theta}(x) = \theta_{0}x_0 + \theta_{1}x_{1} + \cdots + \theta_{n}x_{n}$
가설은 간단히 h(x)로 나타내기도 하며, $x_0$의 값은 항상 1이다.
2. 비용 함수
비용 함수는 가설을 어떻게 세울 것인지를 결정한다. 즉 'θ 값을 어떻게 고를 것인가'를 나타내는 함수다.
기본적인 아이디어는 다음과 같다.
1. 가설의 parameter가 dataset과 얼마나 잘 일치하는가?
다르게 말하면 다음과 같다.
"주어진 데이터 (x, y)의 y값과 가설의 예측값을 가장 가깝게 하는 θ를 선택한다."
즉 예측값과 실제 값의 차이를 최소화하는 θ를 고르는 것이다. 이를 최소화 문제라고도 한다.
2. 비용 함수
비용 함수는 다음과 같다.
여기서
는 i번째 training example을 의미한다.
예를 들어
| 집 크기(m²) | 집 값(₩) |
| 195 | 507840000 |
| 132 | 256128000 |
| 142 | 347760000 |
| 79 | 196512000 |
에서 2번째 training example은 (132, 256128000)이 된다.
위 식은 각 example에 대한 예측 값과 실제 값의 차이를 나타낸다.
그냥 차이의 합이 아니라 차이의 합으로 식을 정의한 이유는 다음과 같다.
① 직선과 실제 데이터의 오차를 표현한다.
② 거리를 구해야 하므로 (예측 값 - 실제 값)의 제곱이 아니라 그냥 절댓값을 취하면 되는데, 그러면 미분불가능한 점이 생길 수 있다. 따라서 제곱한다.
③ 제곱을 미분하면 식 앞에 계수 2가 붙으므로 1/2를 곱한다.
즉 원래는 예측 값과 실제 값의 평균 차이를 나타내는 식이지만 "오차를 표현하는 미분가능한 함수"를 만들려고 하다 보니 위와 같은 식이 만들어졌다. 위 식은 선형 회귀의 목적 함수(특정한 목적에 의해 만들어진 함수)라고도 한다.
또한 θ는 다음을 나타낸다.
즉 비용 함수의 parameter vector라고 볼 수 있다. 따라서 가설 역시 다음과 같이 나타낼 수 있다.
그리고 가설을 세우기 위한 θ(비용 함수를 최소화하는 θ)는 다음과 같이 표기한다.
J(θ)를 최소화(minimize)하는 θ라는 의미다.
이를 토대로 결국 집 값을 예측하는 과정을 도식화하면 다음과 같다.

Learning algorithm의 목표는 가설을 세우기 위한 θ를 찾는 것이다.
'Machine Learning > Machine Learning' 카테고리의 다른 글
| Feature scaling (0) | 2021.02.22 |
|---|---|
| Gradient descent for linear regression (0) | 2021.02.21 |
| Gradient descent (0) | 2021.02.21 |
| Unsupervised learning (0) | 2020.12.20 |
| Supervised learning (0) | 2020.12.20 |


