저번주차 탐색 알고리즘들과는 적용대상이 다름
N-Queens Puzzle
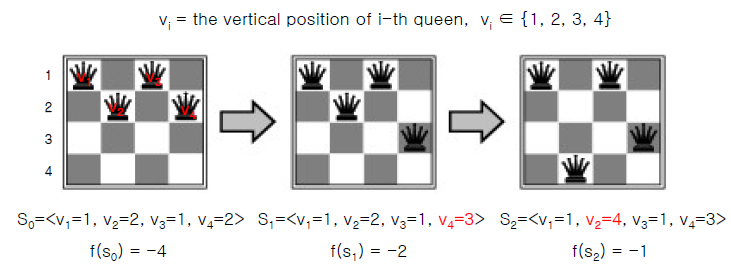
*$f(s_0) = -5$, $f(s_1) = -3$임 (오타)
각 퀸은 같은 행, 열, 대각선 상에 있어서는 안 된다.
각 말을 $v_1$, $v_2$, $v_3$, $v_4$로 본다
각 말 $v_i$는 $i$번째 열 내에서만 움직이므로 행만 지정해주면 된다. -> $v_i \;\in\; \{1, 2, 3, 4\}$
상태 $s_t$는 $<v_1,\; v_2,\; v_3,\; v_4>$로 구성된다.
평가 함수는 문제 안에서 만들어야 한다.
$f(s_i)$은 충돌 횟수다. 예를 들어 $s_0$에서는 다음과 같이 충돌한다.
행: $v_1$-$v_3$, $v_2$-$v_4$
열: 없음
대각선: $v_1$-$v_2$, $v_2$-$v_3$, $v_3$-$v_4$
Local search
평가 함수는 주어진다.
평가 함수가 최대치가 될 수 있는 optimal한 state가 값
항상 하나의 현재 상태를 유지하며 자식 상태를 통해 평가치가 개선되도록 상태를 바꾼다.
개선되지 않으면 그 상태가 답이 됨
Hill-Climbing search

Best-First search 방식, Greedy local search
Greedy: 현재보다 나쁜 상태로는 가지 않음
초기 상태를 랜덤(Random initialization)
$neighbor$: Best인 자식
$current$: 부모 상태
자식 상태와 부모 상태의 평가치를 비교해 자식 상태의 평가치가 더 크면 자식 상태를 현재 상태로 설정
이 경우 Local optimum에 갇히는 문제가 생긴다.

$s_6$이 최적이지만 $s_4$, $s_5$가 $s_2$보다 평가치가 더 작아 이동하지 않게 되므로
Global optimum인 $s_6$에 도달할 수 없고 local optimum인 $s_2$를 반환하게 된다.
이는 초기 상태에도 의존적이다. 만약 출발점을 $s_0$가 아닌 $s_5$로 했다면 $s_6$에 도달했을 것이다.
Simulated annealing search

Local optimum의 문제를 막기 위한 방법(완벽하진 않다)
$T=0$이면 현재 상태 반환
자식 상태의 평가치가 부모 상태보다
크면: $current := next$ (다음 상태로 이동)
작으면: $T$가 점점 작아지므로 $e^{\frac{\Delta E}{T}}$의 확률로 다음 상태로 이동
시간 $t$가 증가함에 따라 Temperature $T$는 감소해 $e^{\frac{\Delta E}{T}}$ 확률이 낮아진다.
$\Delta E <= 0$이므로 $T$가 감소하면 $e^{\frac{\Delta E}{T}}$도 낮아진다.
따라서 $\Delta E <= 0$임에도 자식 상태로 이동하는, 즉 bad move의 확률은 점점 낮아진다.
Local Beam
여러 개의 상태(Random initialization)로 시작해 병렬 탐색함
몇 개는 local optimum에 빠지더라도 한 개 정도는 global optimum을 찾을 수도 있다
-> 한 개의 상태로 시작했을 때보다 Global optimum을 찾을 확률이 더 높다.
매 반복마다 $k$개의 자식 상태가 생성되고 다시 병렬 검색이 진행된다.
$k$개의 상태 중 하나다 goal state에 도달하면 멈추고,
아니면 $k$개의 최선의 자식 상태를 생성한다. 이 때 각 상태들은 다른 상태와 유용한 정보를 주고받는다.
예를 들어 $k=2$라면 다음과 같다.

그런데 $k$개의 상태에서 병렬적으로 탐색한다고 해도 결국 다양성 부족으로 인해 문제를 겪을 수 있다.
이는 Stochastic beam search로 해결할 수 있으며, 이는 유전 알고리즘과 흡사하다.
가능한 경로의 수가 너무 많아서 개수 제한이 필요함
-> 매 반복마다 제일 좋은 $k$개의 상태만 유지($current$는 $k$개만 유지)
-> 이 때 좋은 $k$개는 같은 평가함수로 평가되므로 반복하다보면 다양성이 부족해짐
= 처음에는 다 다른 상태였더라도, 계속 반복하다 보면 비슷한 상태만 남음
= 처음에는 다양성이 있었지만 가장 좋은 $k$개만 남기는 과정을 반복하다보니 bias가 생김(갈수록 다양성을 잃음)
Genetic algorithms(GA)
마찬가지로 무작위로 설정된 $k$개의 상태에서 시작한다.
핵심은 부모 상태와 비슷한 자식 상태를 만드는 것이다.
각 상태는 문자열로 표현되며, 0과 1로 이루어진 벡터로 표현하는 것이 일반적이다.
한 비트는 유전자(gene), 전체 벡터는 염색체(choromosome)으로 표현된다.
평가 함수로 fitness function이 쓰이며, 더 좋은 상태에서 더 높은 값을 가진다
유전 연산(선택, 교배, 돌연변이)을 이용해 다음 세대를 생산한다.
부모 상태 두 개를 선택해서 교배할 때 선택되는 부모는 반드시 평가치가 가장 높은 상태일 필요는 없다.

(b)
$\frac{24}{24 + 23 + 20 + 11} = 31\%$
$\frac{23}{24 + 23 + 20 + 11} = 29\%$
$\frac{20}{24 + 23 + 20 + 11} = 26\%$
$\frac{11}{24 + 23 + 20 + 11} = 14\%$
(c)
Crossover point를 기준으로 문자열을 자르고
(d)
자른 문자열을 섞는다
(e)
돌연변이가 발생해 표시된 부분이 바뀜
-> 부모 상태와 전혀 다른 자식 상태가 됨
-> 부모 상태의 근처에만 있는 상태가 아닌 전혀 다른 상태도 탐색에 포함됨
-> 다양성이 확보된다.
각 자리에서 돌연변이가 발생할 확률은 서로 독립적이다.
따라서 Beam search의 병렬 검색에서 다양성을 확보하게 된다.
'강의노트 > 인공지능' 카테고리의 다른 글
| [인공지능] 7주차: Adversarial Search (0) | 2021.04.13 |
|---|---|
| [인공지능] 5주차: Heuristic search (0) | 2021.03.30 |
| [인공지능] 4주차: 탐색 (0) | 2021.03.23 |
| [인공지능] 3주차: Task environment, Agent type (0) | 2021.03.16 |
| [인공지능] 2주차 (2): Agent (0) | 2021.03.10 |


