Single-Agent Search Problems
Vaccum cleaner
8-Puzzle
Path-finding
n-Queens
...
n-Queens
초기 상태에서 더 좋아지는 상태, 거기서 더 좋아지는 상태, ...
이런 식으로 선택하다가
더이상 좋아질 수 없으면 그게 optimal
이런 문제들은 한 개의 agent가 혼자서 탐색하는 문제임
Adversarial Search Problems
에이전트들의 목표가 상충하는 경쟁적 환경과
그런 환경에서 발생하는 adversarcal search
이런 문제를 Game이라고 한다.
나한테는 이득이 되고 상대한테는 손해가 되도록 하는 행동을 결정하는 방법
경쟁관계이므로 상대의 행동은 예측할 수 없다(unpredictable)
나의 행동은 내가 상대의 행동을 예측하고, 그걸 토대로 결정함
즉 상대의 행동을 예측할 수는 없지만 나처럼 행동한다는 가정 하에 상대의 행동에 대한 예측치를 계산해 행동을 결정한다.
근데 왜 상대의 행동을 예측할 수 없을까...
서운하네....
2-Player Game Search Tree

① 초기 상태는 아무 것도 없는 상태 (9가지)
② X가 하나 놓인 상태 가능한 모든 상태 (8가지)
③ X가 하나 놓이고 O가 하나 놓인 가능한 모든 상태 (7가지)
...
실제로는 가능한 경로들 중 한 경로로 가지만 일단 가능한 모든 경로를 고려해야 함
어떤 경로를 선택하냐에 따라 Terminal state는 다 다를 수 있음(이기거나, 지거나, 무승부거나)
Minimax Search

평가치: 내가 이기면 10, 상대가 이기면 -10, 무승부면 0
자식 노드의 평가치를 기준으로 최대를 최선으로, 최소를 최선으로 간주하는 과정을 반복함
Assumption
ⓐ 상대는 나와 동일한 상태 평가 함수를 갖는다.
ⓑ 상대는 나와 같이 최선의 선택을 한다.
상태 3에서 5로 갈 지 6을 갈 지는 내가 아닌 상대방이 결정하는 것
다만 5 아님 6밖에 없다는 건 알 수 있다
근데 5가 되면 상대방이 이기는(내가 지는) 상태 = Terminal node
내 입장에서는 평가치가 최소(여기서는 -10)임
가정에 의해 상대방은 나와 같이 최선의 선택을 하므로 상대는 평가치가 최소인 상태 5로 갈 것이라고 간주한다.
6이 되면 누가 이기거나 지는 상태가 아님, 이 다음으로 가능한 경우는 9밖에 없음
9가 되면 내가 이김 = Terminal node -> Node 6의 평가치는 10
완전성: Y
여기서 완전성은 '목표 상태에 도달할 수 있는가?'가 아니라
탐색을 통해 루트 노트에서 '어느 상태로 갈 지 결정할 수 있는가'를 나타냄
최적성: Y
'결정된 상태가 최적인가?'를 나타냄
모든 경우의 수 중 최선을 선택하므로 최적임
$b$는 branch의 수
$m$은 가장 깊은 깊이: 결론이 날 때까지 level $m$까지 진행해야 함
시간 복잡도: $O(b^m)$
공간 복잡도: $O(bm)$
근데 실질적으로 적용할 수 없음: 체스는 $b=35$, $m=100$인데 이거 계산할 동안 상대가 기다릴 리가
찾기만 하면 최적인데 현실적으로는 너무 오래 걸림
$b$는 게임의 룰 상 정해진 것이므로 수정할 수 없다
-> $m$을 수정할 수밖에: 깊이 제한을 둔다
근데 좀만 더 가면 최적일 수도 있고 끝까지 안 가면 승패가 결정되지 않을 수도 있는데?
-> 시간 복잡도를 확보하려고 깊이 제한을 둔 만큼 최적의 결정에서 멀어질 수 있다
Time/Resource limits
ⓐ 깊이제한(Depth limit)
ⓑ 탐색절단(Cutoff)
ⓒ 상태 평가 함수(Evaluation function)
으로 해결
Minimax Cutoff Search
제한된 Minimax search
Terminal-test는 Curoff-test로 대체
단말 상태인지 아닌지 검사 -> 깊이제한에 도달했는지 검사
Utility는 Eval로 대체
이기면 +10, 지면 -10 -> Eval(비단말상태 평가 함수)
원래 이기거나 지는 건 단말 상태에서만 평가 가능하나
여기서는 비단말 상태에 대해서도 평가할 수 있어야 함
깊이 제한이 있어도 정확히 결정할 수 있는가?
깊이 제한 4: 사람 기준 초보자
깊이 제한 8: 사람 기준 마스터
깊이 제한 12: 사람 기준 챔피언
Kasparov와 Deep blue의 경기가 깊이 제한 12 수준이었음
Tic-Tac-Toe

$e(p)$
비단말상태 평가 함수
(내가 이길 수 있는 남은 경우의 수) - (상대방이 이길 수 있는 경우의 수)로 정의함
-> $e(p)$의 값이 0이면 무승부, 양수면 내가 유리, 음수면 상대가 유리하다는 뜻
초기 상태에서 O가 이길 수 있는 경우의 수는 대각선은 X가 막고 있어서 안 되고
X를 둘러싼 가로 두 줄 또는 세로 두 줄 뿐
회전해서 같으면 같은 걸로 침(탐색 상에서는 별 차이가 없음)
즉 그림에서 아래의 4개는 다 똑같은 거로 침
Best는 아닐 수 있지만 나쁘지 않은 함수

평가치가 1, -2, -1일 때 각각을 선택해 깊이 2까지 탐색한 후, Backtrack해서 나머지 경로도 탐색 진행
-> 깊이 제한이 있는 깊이 우선 탐색
* 초기 상태가 왜 9개가 아니라 3개인가?
회전해서 같으면 같은 걸로 치니까..
Start node의 1은 자식 노드의 평가치 1, -2, -1 중 최댓값(이게 최선이니까)
일단 내가 더 유리한 상태를 고르되 그 중에서 더 유리한 상태를 고른다: Start node - ① - ②
(원 안의 숫자는 평가치)
Minimax 였다면 Start node - ① - ①로 예측했을 것임
상대도 나와 같이 최선의 결정을 한다고 가정하니까 상대는 자기한테 유리한(나한테 덜 유리한) 상태를 선택한다.
즉 start node - ①까지는 내 선택이고, 그 다음 상대의 선택은 ①일 때 상대에게 더 유리함
따라서 Minimax는 Start node - ① - ①로 예측한다.

마찬가지로 여기서 Start node는 First stage에서 level 2의 상태들 중 평가치가 가장 큰(2) 상태임
따라서 현재 second stage까지는 결정됐고 이제 위의 그림에서 evaluation 값이 가장 큰 third stage를 선택해야 함
α-β Pruning
Minimax Cutoff도 상태 수가 너무 많음
-> 모든 상태를 펼칠 필요가 있을까?
-> 필요없는 건 extend하지 말고 넘어가자

① 깊이 우선 탐색이므로 첫 번째 MIN node의 첫 번째 leaf node까지 진행
② 첫 번째 MIN 노드가 가질 수 있는 값은 커봤자 3(뒤에 뭐가 나오든 3보다 작거나 같은 걸 고르니까)
③ 이 노드의 두 번째 leaf node의 값은 12. MIN은 이 노드를 선택하지 않으므로 여전히 최대값은 3
④ 세 번째 leaf node의 값은 8. 마찬가지로 MIN은 이 노드를 선택하지 않으므로 여전히 최대값은 3
⑤ 첫 번째 MIN 노드의 후행 상태를 모두 조사한 결과 이 노드의 값은 3으로 결정됨.
⑥ 따라서 Root node의 값은 3 이상이라고 '기대'할 수 있다. (기댓값은 3 이상)

① 두 번째 MIN node의 첫 번째 leaf node의 값은 2
② 따라서 MIN node가 가질 수 있는 값은 최대 2다. (뒤에 뭐가 나오든 2보다 작거나 같은 걸 선택할 거니까)
③ 그런데 첫 번째 MIN node가 적어도 3임을 알고 있으므로 MAX node는 이 node를 선택하지 않는다.
④ 따라서 나머지 후행 상태는 조사(확장)하지 않는다.



① 세 번째 MIN node의 첫 번째 leaf node 값은 14.
② 따라서 세 번째 MIN node의 평가치는 최대 14(라고 인식한)다.
③ 그런데 두 번째 leaf node의 값이 5이므로 평가치는 최대 5(라고 인식한)다.
④ 세 번째 leaf node의 값은 2다. 따라서 세 번째 MIN node의 평가치는 정확히 2가 된다.
⑤ 결과적으로 MAX는 root node에서 3의 평가치를 제공하는 첫 번째 MIN node로 진행한다.
* MIN node의 기대치는 상한, MAX node의 기대치는 하한
결과는 Minimax cutoff랑 똑같은데 탐색할 필요가 없는 상태는 탐색하지 않는다는 장점이 있다.
현재 node가 MIN, Root node가 MAX라고 하자.
그리고 현재 node(MIN)의 기대치는 β, 부모 node의 기대치는 α라고 하자.
즉 α는 MAX에 대한 경로에서 지금까지 발견한 최선의 선택 = 값이 가장 큰 선택
β는 MIN에 대한 경로에서 지금까지 발견한 최선의 선택 = 값이 가장 작은 선택
그럼 다음과 같이 나타낼 수 있다.

$node$는 현재 노드를, $ancestor$는 현재 노드의 모든 상위노드를 의미함.
$node$의 leaf node에서 탐색하지 않은 부분이 이 조건에 대응되는 것
반대의 경우는 다음과 같다.


현재 노드가 MIN이면 더 낮은 level의 MAX node와 비교, 현재 노드가 MAX이면 더 낮은 level의 MIN node와 비교,
내가 MIN인 경우 조상 노드의 MAX이 더 크면 확장하지 않음
내가 MAX인 경우 조상 노드의 MIN이 더 작으면 확장하지 않음
: 확장해봤자 조상노드는 현재 자기가 선택한 노드로 진행함
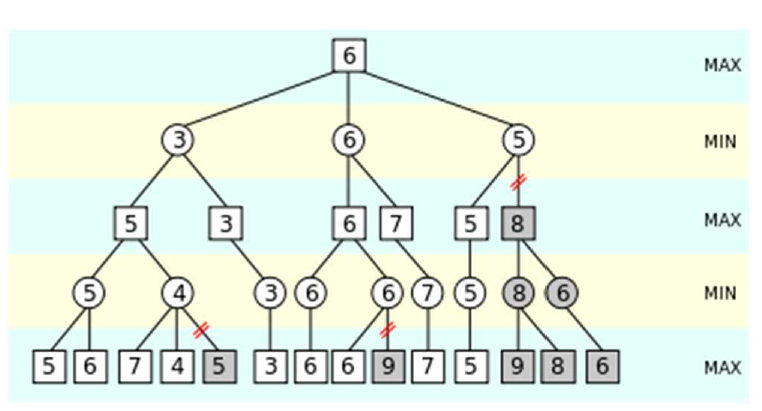
4 // 5:
내가 MIN인데 내 부모 노드는 MAX고 값이 5임
내 값은 leaf node를 조사한 결과 현재 4임
나머지 한 노드의 값이 몇 인지는 알 수 없으나 내 값은 어차피 4 이하고, 그러면 부모노드는 나를 선택하지 않음
따라서 더 진행할 필요가 없다.
α-β pruning은 상태 조사 순서에 의존한다.
즉 어떤 후행자를 선택하는가에 따라 쳐내는 노드의 수가 달라지므로 효율도 달라진다.
= 최선의 후행자가 존재한다
+ pruning 가능한지 매번 체크해야 함
= 매번 조상 노드와 비교해야 됨
=> 항상 유리하지는 않다.
상태 공간이 크면 모르지만 작을 때는 그냥 Minimax cutoff가 나음
Negamax algorithm
MAX를 구했다가 MIN을 구했다가 번갈아서 하기 귀찮다
-> 음수로 통일하자
-> 음수로 바꾼 결과 최대인 것
자식 상태의 평가치를 음수로 바꿈(negate)
그러면 한 가지 방법으로 평가치를 비교할 수 있음
즉 MAX()랑 MIN() 두 개의 함수를 쓸 필요가 없음
|
1
2
3
4
5
6
7
|
function negamax(node, depth, color) is
if depth = 0 or node is a terminal node then
return color × the heuristic value of node
value := −∞
for each child of node do
value := max(value, −negamax(child, depth − 1, −color))
return value
|
cs |
$node$: 현재 상태
$depth$: 깊이 제한
$color$: MAX를 취할 건지 MIN을 취할 건지 비교
$color = 1$이면 자식 상태는 negate됨 (호출부의 -color)
깊이 제한에 걸리면 node의 평가치(heuristic value)와 color의 곱 반환
$color = 1 \rightarrow MAX$이 구해짐
$color = -1 \rightarrow MIN$이 구해짐
즉 현재 node의 color 값이 1이면 부모 노드에는 MAX가 들어감

한 줄 요약) $max(a,\;b) = -min(-a,\; -b)$
'강의노트 > 인공지능' 카테고리의 다른 글
| [인공지능] 6주차: Local search algorithms (0) | 2021.04.06 |
|---|---|
| [인공지능] 5주차: Heuristic search (0) | 2021.03.30 |
| [인공지능] 4주차: 탐색 (0) | 2021.03.23 |
| [인공지능] 3주차: Task environment, Agent type (0) | 2021.03.16 |
| [인공지능] 2주차 (2): Agent (0) | 2021.03.10 |


